
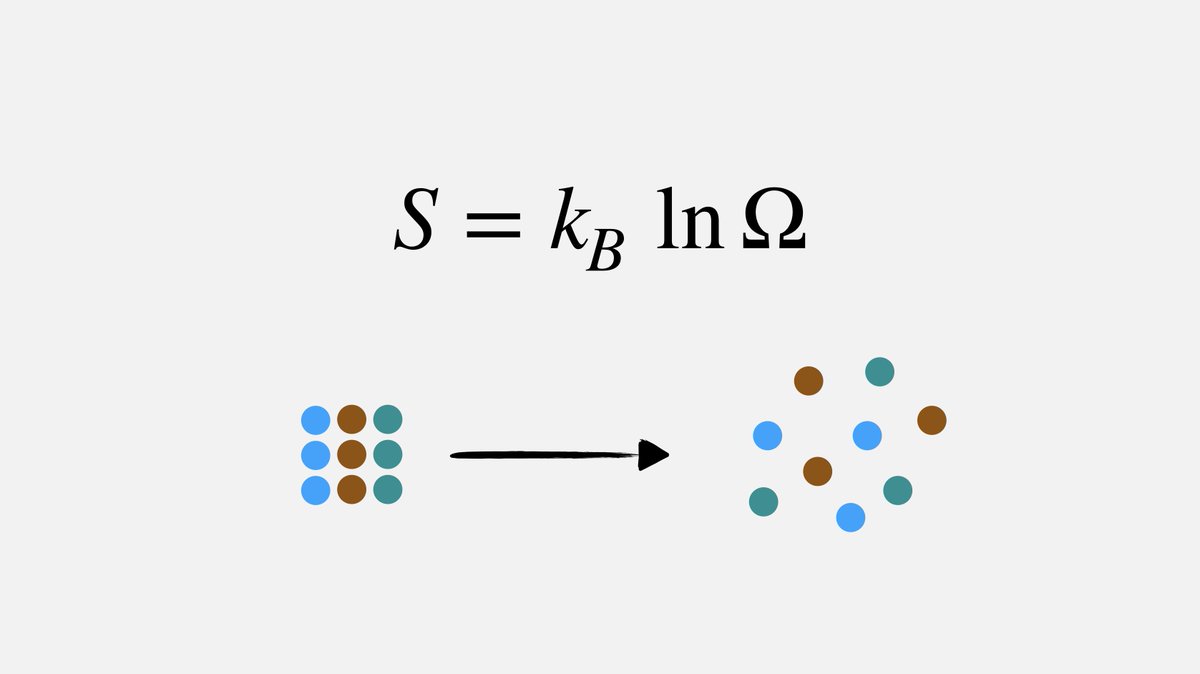
The Boltzmann Equation Figure 18.2 “Ludwig Boltzmann” Figure 18.1 “Two-Atom, Double-Flask Diagram.” When the stopcock is opened between the flasks, the two atoms can distribute in four possible ways. Thus we can say that it is entropically favoured for the gas to spontaneously expand and distribute between the two flasks, because the resulting increase in the number of possible arrangements is an increase in the randomness/disorder of the system. If we increased the number of atoms, we would see that the probability of finding all of the atoms in the original flask would decrease dramatically following (½) n, where n is the number of atoms.

The likelihood of all atoms being found in their original flask, in this case, is only 1 in 4. If we were to take snapshots over time, we would see that these atoms can have four possible arrangements.
Law of entropy free#
When the stopcock is opened, both atoms are free to move around randomly in both flasks. At first, both atoms are contained in only the left flask. In this system, we have placed two atoms of gas, one green and one blue. The Molecular Interpretation of EntropyĬonsider the following system, where two flasks are sealed together and connected by a stopcock (Figure 18.1 “Two-Atom, Double-Flask Diagram”). These definitions can seem a bit vague or unclear when you are first learning thermodynamics, but we will try to clear this up in the following subsections. But what exactly is entropy? Entropy is typically defined as either the level of randomness (or disorder) of a system or a measure of the energy dispersal of the molecules in the system. The second law of thermodynamics states that a spontaneous process will increase the entropy of the universe. To assess the spontaneity of a process we must use a thermodynamic quantity known as entropy ( S). To be able to estimate change in entropy qualitatively.To gain an understanding of the Boltzmann equation and the term microstates.To gain an understanding of the term entropy.


 0 kommentar(er)
0 kommentar(er)
